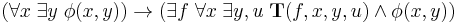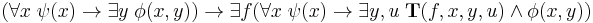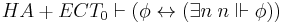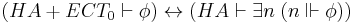Church's thesis (constructive mathematics)
In constructive mathematics, Church's thesis is the mathematical assertion that all total functions are recursive. It gets its name after the informal Church–Turing thesis, which states that every algorithm is in fact a recursive function, but the constructivist version is formal and much stronger. It is in fact incompatible with classical logic.
Formal statement
One way Church's Thesis can be formally stated is by the schema:
Where the variables range over the natural numbers, and  is any predicate. This schema asserts that, if for every x there is a y satisfying some predicate, then there is in fact an f which is the Gödel number of a general recursive function which will, for every x, produce such a y satisfying that predicate. (T is some universal predicate which decodes the Gödel-numbering used.)
is any predicate. This schema asserts that, if for every x there is a y satisfying some predicate, then there is in fact an f which is the Gödel number of a general recursive function which will, for every x, produce such a y satisfying that predicate. (T is some universal predicate which decodes the Gödel-numbering used.)
The thesis is incompatible with classical logic; adding it to Heyting arithmetic (HA) allows one to disprove instances of the law of the excluded middle. For instance, it is a classical tautology that every Turing machine either halts or does not halt on a given input; but if that were true, then from Church's Thesis one would conclude that there is a general recursive function which solves the halting problem. This is impossible.
However, Heyting arithmetic is equiconsistent with Peano arithmetic (PA) as well as with Heyting arithmetic plus Church's thesis. That is, adding either the law of the excluded middle or Church's thesis can not make Heyting arithmetic inconsistent, but adding both will.
Extended Church's thesis
Extended Church's thesis (ECT) extends the claim to functions which are totally defined over a certain type of domain. It is used by the school of constructive mathematics founded by Andrey Markov Jr. It can be formally stated by the schema:
In the above,  is restricted to be almost-negative. For first-order arithmetic (where the schema is designated
is restricted to be almost-negative. For first-order arithmetic (where the schema is designated 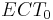 ), this means
), this means  cannot contain any disjunction, and existential quantifiers can only appear in front of
cannot contain any disjunction, and existential quantifiers can only appear in front of 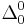 (decidable) formulas.
(decidable) formulas.
This thesis can be characterised as saying that a sentence is true if and only if it is computably realisable. In fact this is captured by the following meta-theoretic equivalences[1]:
Here, 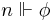 stands for "
stands for "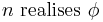 ". So, it is provable in
". So, it is provable in 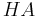 with
with 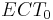 that a sentence is true iff it is realisable. But also,
that a sentence is true iff it is realisable. But also,  is provably true in
is provably true in 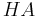 with
with 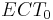 iff
iff  is provably realisable in
is provably realisable in 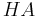 without
without 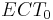 .
.
The second equivalence can be extended with Markov's principle (M) as follows:
So,  is provably true in
is provably true in 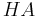 with
with 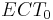 and
and  iff there is a number n which provably realises
iff there is a number n which provably realises  in
in 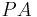 . The existential quantifier has to be outside
. The existential quantifier has to be outside 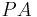 in this case, because PA is non-constructive and lacks the existence property.
in this case, because PA is non-constructive and lacks the existence property.
Reference
- ^ Troelstra, A. S. Metamathematical investigation of intuitionistic arithmetic and analysis. Vol 344 of Lecture notes in mathematics; Springer, 1973